Introduction
The intersection of artificial intelligence and quantum mechanics represents one of the most exciting frontiers in computational science. As quantum systems grow in complexity, traditional computational methods struggle with the exponential scaling of quantum states—a challenge known as the curse of dimensionality. AI algorithms, particularly neural networks and machine learning techniques, are emerging as powerful tools to tackle these computational bottlenecks, enabling researchers to simulate, predict, and understand quantum mechanical systems with unprecedented efficiency.
This article explores the landscape of AI-driven approaches to quantum mechanics computations, examining how modern machine learning techniques are revolutionizing our ability to model everything from molecular dynamics to many-body quantum systems.
The Computational Challenge of Quantum Mechanics
The Exponential Wall
Quantum mechanics describes nature at its most fundamental level, but simulating quantum systems computationally is notoriously difficult. A quantum system with N particles requires describing a wavefunction in a Hilbert space whose dimension grows exponentially with N. For example, a system of 50 quantum spins has 2^50 possible states—over a quadrillion configurations to track simultaneously.
Traditional methods like exact diagonalization become computationally intractable for systems with more than about 20-30 particles. Even sophisticated techniques like quantum Monte Carlo or density functional theory have limitations in accuracy, applicability, or computational cost. This is where AI algorithms enter the picture, offering new paradigms for representing and computing quantum states.
Neural Network Quantum States
Variational Approaches
One of the most promising developments in recent years is the use of neural networks to represent quantum wavefunctions directly. This approach, pioneered by researchers including Giuseppe Carleo and Matthias Troyer, uses artificial neural networks as variational ansätze for quantum many-body states.
The key insight is that neural networks are universal function approximators—they can, in principle, represent any function given sufficient parameters. A quantum wavefunction is ultimately just a complex-valued function mapping configurations to probability amplitudes, making it a natural target for neural network representation.
Restricted Boltzmann Machines
Restricted Boltzmann Machines (RBMs) were among the first neural network architectures applied to quantum state representation. An RBM consists of visible units (representing the quantum configuration) and hidden units (capturing quantum correlations) connected by weighted edges. The wavefunction amplitude for a configuration is computed by summing over all hidden unit states, weighted by the learned parameters.
RBMs have successfully represented ground states of various quantum spin models, including the challenging transverse-field Ising model and Heisenberg antiferromagnets. Their ability to capture both short-range and long-range correlations through the hidden layer makes them particularly suitable for quantum systems exhibiting complex entanglement structures.
Convolutional and Recurrent Architectures
Building on the RBM foundation, researchers have explored more sophisticated architectures:
Convolutional Neural Networks (CNNs) leverage the spatial structure present in many quantum systems, such as lattice models. By using convolutional layers, these networks can efficiently capture local correlations while maintaining translational invariance—a symmetry often present in condensed matter systems.
Recurrent Neural Networks (RNNs) and their variants, including Long Short-Term Memory (LSTM) networks, treat quantum configurations as sequences. This sequential representation is particularly natural for one-dimensional quantum systems and can efficiently encode the causal structure of quantum wavefunctions.
Transformer Models
Most recently, transformer architectures—the same technology powering large language models—have been adapted for quantum state representation. Transformers use attention mechanisms to capture long-range correlations, making them well-suited for highly entangled quantum states. Their ability to handle variable-length inputs and their parallel processing capabilities offer computational advantages over recurrent architectures.
Variational Monte Carlo with Neural Networks
The Variational Principle
Neural network quantum states are typically optimized using the variational principle: the expectation value of the Hamiltonian with respect to any trial wavefunction provides an upper bound to the true ground state energy. By minimizing this energy with respect to the neural network parameters, we approach the true ground state.
The optimization process resembles training a neural network for supervised learning, but with a crucial difference: instead of labeled data, we use the quantum mechanical Hamiltonian as the loss function. This unsupervised approach allows the network to discover quantum states without requiring prior knowledge of the solution.
Sampling and Optimization
Computing the energy expectation value requires sampling from the probability distribution defined by the wavefunction. Markov Chain Monte Carlo (MCMC) methods, particularly the Metropolis-Hastings algorithm, are used to generate representative samples from this distribution.
The optimization itself typically employs stochastic gradient descent or more sophisticated variants like Adam or natural gradient descent. The stochastic reconfiguration method, which approximates the natural gradient using the quantum geometric tensor, has proven particularly effective for quantum state optimization.
Solving the Schrödinger Equation with Deep Learning
Physics-Informed Neural Networks
Physics-Informed Neural Networks (PINNs) represent a different paradigm: instead of representing the wavefunction variationally, they directly solve the Schrödinger equation by encoding physical laws into the loss function. The neural network outputs the wavefunction, and its training loss includes terms enforcing the Schrödinger equation, boundary conditions, and normalization constraints.
This approach has successfully solved quantum mechanics problems including the quantum harmonic oscillator, hydrogen atom, and molecular systems. PINNs offer the advantage of providing differentiable solutions, enabling gradient-based analysis of quantum properties.
Neural Differential Equations
Neural ordinary differential equations (Neural ODEs) extend this concept by treating neural networks as continuous dynamical systems. For time-dependent quantum mechanics, this approach can learn the time evolution operator, predicting how quantum states evolve under various Hamiltonians. This is particularly valuable for studying non-equilibrium quantum dynamics and quantum control problems.
Machine Learning for Density Functional Theory
Functional Approximation
Density Functional Theory (DFT) is the workhorse of computational quantum chemistry and materials science, but its accuracy depends critically on the exchange-correlation functional—a quantity that must be approximated. Machine learning offers new approaches to developing more accurate functionals.
Neural networks trained on high-accuracy quantum chemistry data can learn complex exchange-correlation functionals that go beyond traditional approximations like LDA (Local Density Approximation) or GGA (Generalized Gradient Approximation). These learned functionals can achieve chemical accuracy while maintaining the computational efficiency that makes DFT practical for large systems.
Predicting Molecular Properties
Beyond improving functionals, ML models can directly predict quantum mechanical properties from molecular structure. Graph neural networks, which naturally represent molecular topology, have achieved remarkable success in predicting:
- Ground state energies
- Molecular geometries and conformations
- Electronic excitation spectra
- Reaction barriers and pathways
- Band structures and electronic properties of materials
Models like SchNet, PhysNet, and DimeNet use message-passing algorithms on molecular graphs to capture the quantum mechanical environment of each atom, achieving accuracy comparable to expensive quantum chemistry calculations at a fraction of the computational cost.
Quantum Circuit Optimization
Variational Quantum Algorithms
As quantum computers advance, variational quantum algorithms like VQE (Variational Quantum Eigensolver) and QAOA (Quantum Approximate Optimization Algorithm) require classical optimization of quantum circuit parameters. Machine learning techniques enhance these algorithms by:
- Meta-learning circuit architectures: Neural networks can learn which quantum gate sequences are most effective for specific problem types
- Parameter initialization: ML models trained on previous optimizations can provide good starting points for new problems
- Error mitigation: Neural networks can learn to correct errors in noisy quantum computations
Quantum Circuit Synthesis
Deep reinforcement learning has been applied to automatically design quantum circuits for specific tasks. An agent learns to select and arrange quantum gates to implement desired unitary operations, often discovering more efficient circuits than human-designed alternatives.
Generative Models for Quantum States
Generative Adversarial Networks
Generative Adversarial Networks (GANs), which have revolutionized image and text generation, are being adapted for quantum state generation. A generator network creates quantum states, while a discriminator distinguishes them from samples from a target distribution. This adversarial training can prepare complex quantum states that would be difficult to construct otherwise.
Normalizing Flows
Normalizing flows provide an alternative generative approach with exact likelihood evaluation. By composing a series of invertible transformations, these models can map simple distributions to complex quantum state distributions. The invertibility ensures efficient sampling and exact probability computation—crucial for quantum applications.
Autoregressive Models
Autoregressive neural networks, which generate outputs sequentially by conditioning each component on previous ones, naturally capture the causal structure of quantum measurements. These models have shown impressive results in representing quantum states of spin chains and fermion systems, with particularly efficient sampling properties.
Neural Network Molecular Dynamics
Potential Energy Surfaces
Traditional molecular dynamics relies on accurate potential energy surfaces (PES), typically computed from quantum mechanics for each atomic configuration. This creates a computational bottleneck: quantum calculations are expensive, limiting simulation timescales and system sizes.
Neural network potentials offer a solution by learning the mapping from atomic positions to energies and forces. Once trained on quantum mechanical data, these potentials enable molecular dynamics simulations with near-quantum accuracy at classical computational cost. Models like DeePMD, ANI, and SchNet have achieved remarkable transferability, accurately describing molecules and materials far beyond their training distributions.
Reactive Dynamics and Phase Transitions
Neural network potentials are particularly transformative for reactive chemistry and materials under extreme conditions, where bond breaking and formation make simple empirical potentials inadequate. ML potentials trained on ab initio molecular dynamics can capture complex chemical reactions, catalytic processes, and phase transitions with quantum mechanical fidelity.
Quantum State Tomography
Reconstructing Density Matrices
Quantum state tomography—reconstructing the density matrix of a quantum system from measurements—suffers from exponential scaling in the number of measurements required. Neural networks can dramatically reduce this burden through compressed sensing and representation learning.
A neural network can learn to represent the density matrix using far fewer parameters than the full exponential description, with measurement outcomes used as training data. This approach has successfully reconstructed states of systems with dozens of qubits using orders of magnitude fewer measurements than traditional tomography.
Measurement Optimization
Reinforcement learning algorithms can optimize which measurements to perform, adaptively choosing measurement bases that maximize information gain. This active learning approach to tomography has demonstrated exponential speedups for certain quantum state classes.
Fermion and Boson Systems
Antisymmetry and Symmetry Constraints
Representing fermionic systems (like electrons) requires respecting the Pauli exclusion principle: wavefunctions must be antisymmetric under particle exchange. Neural networks must be carefully designed to maintain this constraint. Several approaches have emerged:
FermiNet: Explicitly antisymmetrizes neural network outputs using determinants Permutation-equivariant networks: Build antisymmetry into the architecture through specialized layers Group-theoretic approaches: Leverage representation theory to construct symmetric and antisymmetric neural networks
For bosonic systems (like photons or certain atoms), wavefunctions must be symmetric, requiring similar but opposite constraints.
Second Quantization Representations
In second quantization, quantum states are described by occupation numbers rather than particle positions. Neural networks working in this representation, often called neural quantum states in occupation number basis, have successfully modeled Hubbard models, quantum chemistry in basis set representations, and quantum optics systems.
Excited States and Spectroscopy
Beyond Ground States
While ground state calculations have received the most attention, excited states are crucial for understanding spectroscopy, photochemistry, and transport properties. Neural network approaches to excited states include:
Orthogonalization constraints: Training multiple neural networks simultaneously with orthogonality constraints to represent different eigenstates Quantum Subspace Methods: Using neural networks to represent a low-dimensional subspace containing the states of interest Time-dependent methods: Learning the full time evolution operator and extracting excited states through Fourier analysis
Predicting Spectra
Machine learning models can directly predict spectroscopic properties from molecular structure. Neural networks trained on experimental or computational spectroscopic data can predict UV-vis absorption, infrared and Raman spectra, NMR chemical shifts, and X-ray absorption spectra, accelerating materials discovery and molecular design.
Open Quantum Systems
Dissipation and Decoherence
Real quantum systems interact with their environment, leading to dissipation and decoherence. Modeling open quantum systems requires describing mixed states and non-unitary evolution, typically through master equations or path integral approaches.
Neural networks can represent density matrices of open systems, learning the effects of environmental coupling without explicitly simulating all environmental degrees of freedom. This coarse-graining approach has successfully modeled quantum systems coupled to thermal baths, photonic environments, and other complex reservoirs.
Quantum Control
Optimal control of quantum systems—manipulating them to achieve desired states or perform specific operations—is crucial for quantum technologies. Reinforcement learning algorithms have demonstrated remarkable success in discovering control protocols for:
- Quantum state preparation
- Quantum gate implementation
- Error correction
- Quantum annealing optimization
These AI-discovered protocols often outperform human-designed control sequences, finding non-intuitive solutions that exploit quantum mechanical features.
Challenges and Limitations
Interpretability
A significant challenge with neural network approaches is interpretability. While these models may accurately represent quantum states or predict properties, understanding why they work and what physical insights they encode remains difficult. This “black box” nature contrasts with traditional quantum mechanics methods where approximations have clear physical interpretations.
Training Data Requirements
Many ML approaches require substantial training data, which for quantum systems must come from expensive quantum chemistry calculations or experiments. The data efficiency of quantum ML models—their ability to learn from limited examples—remains an active research area.
Extrapolation and Transferability
Neural networks can fail catastrophically when extrapolating beyond their training distribution. For quantum chemistry applications, this raises concerns about whether models trained on small molecules can reliably describe larger systems or different chemical environments. Ensuring transferability requires careful architectural choices and training strategies.
Computational Cost
While neural network potentials are faster than ab initio calculations, they still have computational overhead compared to simple empirical potentials. For very large-scale simulations, this cost can be prohibitive. Additionally, training neural networks for quantum systems often requires specialized hardware (GPUs or TPUs) and expertise.
Future Directions
Quantum-Classical Hybrid Algorithms
The future likely involves tight integration of classical AI algorithms with quantum computers. Quantum processors could generate training data or perform specific subroutines, while classical neural networks handle optimization and post-processing. This synergy could overcome limitations of both purely classical and purely quantum approaches.
Foundation Models for Quantum Systems
Inspired by large language models, researchers are developing “foundation models” for quantum chemistry and materials science—large neural networks pre-trained on diverse quantum mechanical data. These models could be fine-tuned for specific applications, dramatically reducing the data and computation required for new problems.
Automated Discovery
AI algorithms could autonomously discover new quantum algorithms, materials, or molecular designs. Combining neural network surrogate models with evolutionary algorithms or Bayesian optimization enables exploring vast chemical and parameter spaces, potentially uncovering materials with unprecedented properties or new quantum phenomena.
Physics-Constrained Architectures
Future neural network architectures will increasingly incorporate physical constraints and symmetries directly into their structure. Rather than learning from scratch, these networks would start with encoded physical knowledge, requiring less data and improving generalization. Group-equivariant neural networks and gauge-equivariant networks represent early examples of this direction.
Conclusion
AI algorithms are fundamentally transforming computational quantum mechanics, offering solutions to problems once considered intractable. Neural network quantum states, machine learning potentials, and deep learning approaches to the Schrödinger equation represent just the beginning of this revolution.
As quantum systems grow in complexity—from larger molecules to quantum computers with hundreds of qubits—the role of AI will only expand. The synergy between quantum mechanics and artificial intelligence promises not just computational efficiency, but deeper understanding of quantum phenomena and new capabilities for quantum technology.
The field remains young and rapidly evolving. Many fundamental questions remain open: What are the ultimate limits of neural network representations for quantum states? Can we develop quantum ML algorithms that are both accurate and interpretable? How can we best combine domain knowledge with data-driven learning?
What’s clear is that the marriage of AI and quantum mechanics will continue yielding groundbreaking developments, pushing the boundaries of what we can compute, predict, and ultimately understand about the quantum world that underlies all of reality.
The integration of artificial intelligence into quantum mechanics computation represents not just a technical advancement, but a paradigm shift in how we approach some of science’s most fundamental questions. As these methods mature and merge with emerging quantum computing technologies, we stand at the threshold of a new era in computational science.



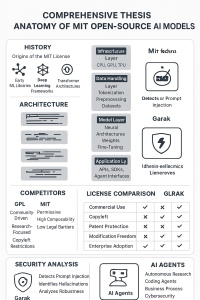
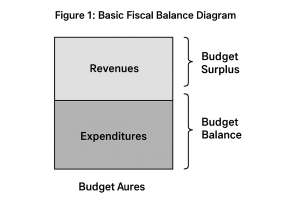
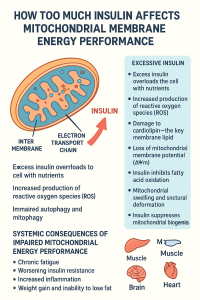
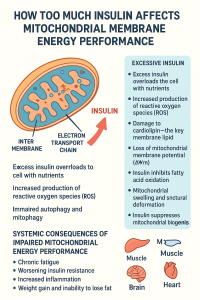
Be First to Comment